1. 백트래킹? DFS? 백트래킹과 DFS는 어떻게 보면 분리하기가 애매한 개념이다. 굳이 분리해서 의미를 부여하자면 끝까지 가느냐 돌아오느냐로 간단하게 생각해볼 수 있다. DFS 역시 재귀를 통해서 구현하므로 시작 기점으로 돌아오는 개념이 들어가 있기는 하지만, 백트래킹의 경우 현재 가는 길이 더 이상의 해가 아니라고 판단되면 되돌아오는 것을 의미한다. 간단하게 DFS 개념을 정리하자면, 가능한 모든 경로를 깊이 우선으로 탐색하는 것을 의미한다. DFS에 대한 자세한 내용은 아래 게시글을 통해 알아보자! DFS(Depth-First Search) + BFS 복습 깊이 우선 탐색(DFS, Depth-First Search)을 알아보기 이전에 그래프에 대한 개념을 이해해야 하므로, 먼저 아래 포스팅을 참고..
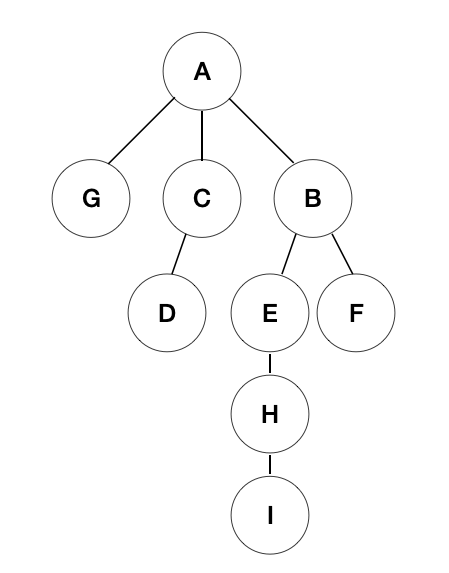
깊이 우선 탐색(DFS, Depth-First Search)을 알아보기 이전에 그래프에 대한 개념을 이해해야 하므로, 먼저 아래 포스팅을 참고하도록 하자. 그래프와 BFS(Graph & Breadth First Search) BFS(너비 우선 탐색) 알고리즘에 대해 알아보기 전에 필수적으로 알아봐야 할 자료구조는 바로 그래프(Graph)다. 그래프는 실질적으로 프로그래밍 언어 라이브러리 상에서 제공하기 보다는 추상적 kwanik.tistory.com 1. 깊이 우선 탐색(DFS, Depth-First Search) 이전 포스트와 '깊이 우선 탐색'이라는 이름에서 알 수 있듯이, '깊이 우선 탐색'은 먼저 한 방향으로 갈 수 있는 경로를 먼저 탐색하는 방식이다. 이는 그래프 탐색의 가장 단순하면서도 고전적..
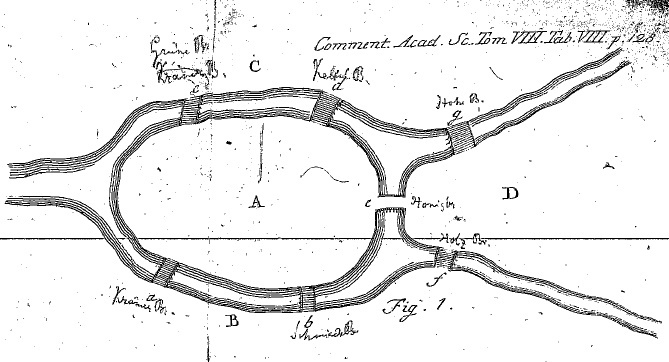
BFS(너비 우선 탐색) 알고리즘에 대해 알아보기 전에 필수적으로 알아봐야 할 자료구조는 바로 그래프(Graph)다. 그래프는 실질적으로 프로그래밍 언어 라이브러리 상에서 제공하기 보다는 추상적인 자료구조로써 개념을 차용하여 알고리즘에 응용하여 푸는 경우가 많으므로, 자료구조 카테고리가 아닌 알고리즘 카테고리에서 함께 다루고자 한다. 그래프 그래프의 정의 및 개념 그래프(G)는 정점 집합(V)과 간선 집합(E)으로 구성된 자료구조로, 대상과 대상 간의 관계를 나타내는 자료구조다. 그래프는 다들 너무나도 익숙하게 들어봤을 '쾨니히스베르크(Königsberg) 다리'를 보고 수학자 오일러가 '한붓그리기' 문제를 해결하기 위해 고안한 것으로 알려져 있기도 하다. 이 고안법에서 중요한 것은, 각 육지를 잇는 다..
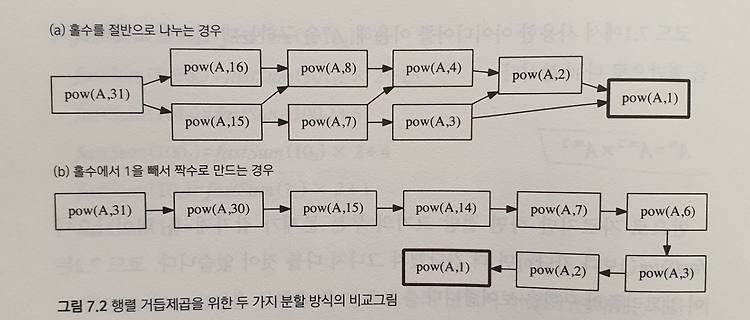
특정한 문제를 풀이함에 있어 큰 문제를 작은 문제로 나뉘어서 푸는 방법들에 대해서는 앞선 포스트들을 통해 계속해서 언급하였다. 오늘 다룰 분할정복(Divide & Conquer)은 그 패러다임을 가장 직관적으로 다루는 테크닉이라고 볼 수 있다. 주어진 문제를 둘 이상의 부분 문제로 나눈 뒤 각 문제에 대한 답을 계산하고, 각 부분 문제의 답으로부터 전체 문제의 답을 계산해내는 것 분할정복은 아래의 세 구성요소로 다시 생각해볼 수 있다. Divide : 문제를 더 작은 문제로 분할하기 Merge : 각 문제의 답을 원래 문제에 대한 답으로 병합 Base Case : 더 이상 분할하지 않고 곧장 풀 수 있는 매우 작은 문제 세 구성요소에 대해서는 부가적인 설명이 필요없을 것으로 보이나, 분할정복으로 특정 문..
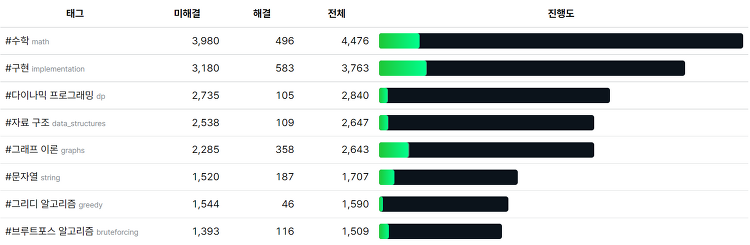
동적 계획법은 정말 가장 많이 대회에서 출제되는 문제 유형임과 동시에 반드시 알아야만 하는 내용이기도 하다. 명확하게 '이것이 동적 계획법 문제다' 라고 분류하기 보다는 앞선 브루트 포스나 그리디 알고리즘과 같이 문제를 풀어나가는 하나의 방법으로 접근하는 것이 올바르다고 생각한다. 동적 계획법 역시 큰 문제를 작은 문제로 나누는 것에서 출발한다. 지금까지의 내용을 정리하면 아래와 같다. 브루트 포스(Brute Force): 작은 문제 하나하나 다 살펴볼거야! 탐욕법(Greedy): 작은 문제마다 답을 선택해 버릴거야! 그렇다면 동적 계획법의 메커니즘은 어떤 것일까? 다른 작은 문제에서 만들어 놓은 값을 다시 쓸거야! 즉, 작은 문제들로 분류하여 연산을 하는 과정에서 같은 연산을 반복적으로 수행해야 한다면..
앞선 알고리즘 소개 포스트를 통해 완전 탐색을 알아보았는데, 완전 탐색(brute force)의 핵심은 큰 문제를 작은 문제로 분할하여 모든 경우를 탐색해보는 것이었으며 그 중, 작은 문제로의 분할이 가장 핵심이라고 볼 수 있다. 이는 비단 완전 탐색에 국한되는 것이 아니라 향후 다룰 동적 계획법(Dynamic Programming)이든, 지금 다룰 욕심쟁이 알고리즘이든 모든 알고리즘 문제의 가장 기본이 된다고 볼 수 있다. 완전 탐색이 모든 경우에 대해 체크한 후 최적의 해를 골라내는 것이었다면, 욕심쟁이 혹은 탐욕법(Greedy)의 경우 각 단계마다 현재 최선의 방법만을 선택하는 것을 의미한다. 다만 늘 현재의 최선의 해답만을 선택하므로, 앞으로 남은 선택지들에 대한 사항은 고려하지 않게 되는데 이로..

다양한 알고리즘 문제들을 풀이하는 방법들이 있는데 그 중 첫 번째는 역시 브루트 포스(Brute Force) 가 아닐까 싶다. 해킹 기법 중 가장 기본적인 공격 방식 중에 '무차별 대입 공격(brute-force attack)'이라는 것이 있는데, 이는 특정한 암호를 풀기 위해 가능한 모든 값을 대입하는 방식을 의미한다! 쉽게 생각하자면 아래 자전거 자물쇠를 살펴보면 된다. 이 자전거 자물쇠를 푸는 가장 쉬운 방법은 '0000' 부터 '9999'까지 하나씩 돌려보면 될 것이다. 브루트 포스(brute force) 알고리즘 역시 마찬가지다. 다른 말로 '무식하게 풀기'라고도 하는데, 특정한 문제에 발생 가능한 경우의 수를 일일이 나열하면서 답을 찾는 것이다. 최단 거리를 찾기 위해 노드 간의 경로들을 일일..
개요 비트마스크(BitMask) 기법에 대해 이해하고 활용할 수 있는 능력을 키운다. 비트마스크는 알고리즘 카테고리에 들어와 있기는 하지만 알고리즘이라기 보다는 일종의 테크닉에 가깝다. 1. 비트(Bit) 그리고 비트연산 컴퓨터에서 사용되는 데이터의 최소 단위인 비트(Bit)는 '0과 1'의 값을 가질 수 있다. 이 때, 0은 'false / 꺼져 있음(off)' 그리고 1은 'true / 켜져 있음(on)'를 각각 나타낸다. 1111 1111 = 255 각 비트의 의미를 잘 기억해두고 우선 비트를 조작할 수 있는 비트 연산을 먼저 간단하게 정리해본다. 1) AND 연산(&) 논리 연산자인 &&과 마찬가지로 두 비트가 모두 1일 경우 1을 반환한다. 1001 & 1111 = 1001 2) OR 연산( |..